Summary
Set the sUSDe-long-v2 LlamaLend monetary policy to Semilog deployed here with min/max params set to 0.004% / 47.658%.
Motivation
- Secondary Monetary Policy imposes artificial rate caps, limiting effective risk management by introducing an external dependency to assign market rates.
- High interest rates serve as vital signals, reflecting actual market risk and promoting system stability.
- A Semilog IRM allows responsive, dynamic interest rate adjustments, effectively discouraging excessive borrowing during market stress and encouraging timely repayments.
- Market-driven dynamics will naturally regulate interest rates, promoting sustainable performance based on conditions internal to the lend market.
The current SecondaryMP interest rate model for sUSDe is pegged externally to the sUSDe APR, thus imposing a rigid ceiling on maximum LlamaLend interest rates based on sUSDe revenue distribution. While intended to regulate borrowing costs with respect to the sUSDe yield trends, this model increases systemic risks for LlamaLend, exposing it to additional external dependencies.
Enhancing Risk Mitigation: Prioritizing Lenders
LlamaLend must prioritize lender protection to minimize the risk of accruing bad debt. Persistent maximum utilization (such as seen in the past in former SecondaryMP Market) often signals systemic distress.
Under current SecondaryMP conditions, artificially capped APRs limit the protocol’s ability to discourage borrowing and stimulate repayments effectively, exacerbating potential illiquidity and bad debts if underlying assets depreciate. For instance, if sUSDe experiences significant volatility or begins to depeg, borrowers could exploit the artificially limited APR by maximizing borrowing, liquidating collateral such as crvUSD, and abandoning positions.
By contrast, SemilogMP assigns rates purely according to the LlamaLend market’s utilization and min/max bounds assigned by DAO governance. This offers the Curve DAO more direct control over supply/demand regulation. Eliminating external rate referencing enables organic market self-correction through inherent supply and demand mechanisms, minimizing vulnerability to exploitation and unforeseen systemic risks. Given this, we advocate for the sUSDe transition to a Semilog Interest Rate Model.
sUSDe Semilog Model Parameterization Analysis
To accurately identify safe and effective market-driven interest rates, we employed our simulation framework for IRM parameter optimization.
Detailed methodology: LlamaLend Monetary Policy Optimization
sUSDe-long IRM Analysis and Results
sUSDe-long-v2 is currently deployed on Ethereum with controller address: 0xB536FEa3a01c95Dd09932440eC802A75410139D6. The current IRM is a SecondaryMP model referencing sUSDe yield externally.
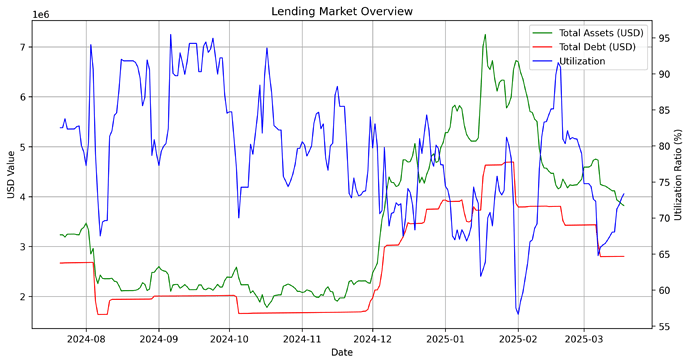
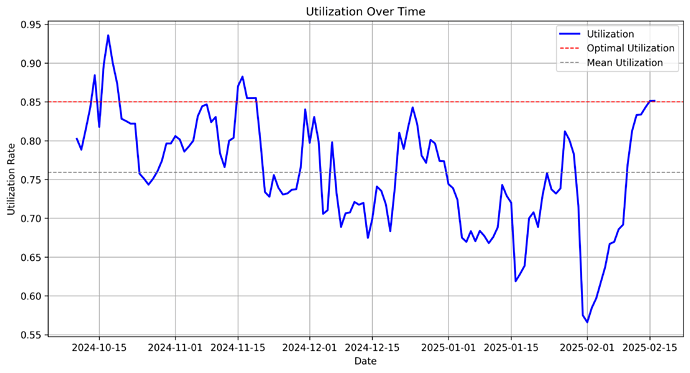
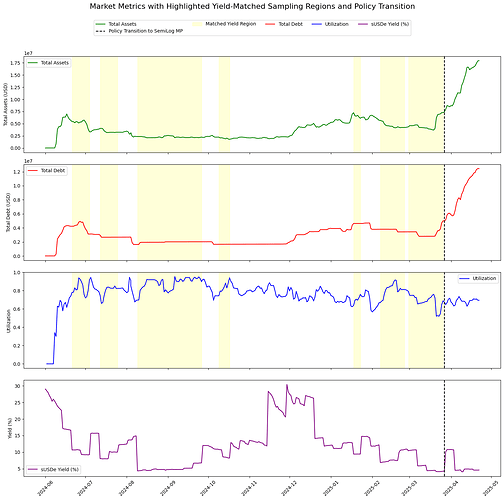
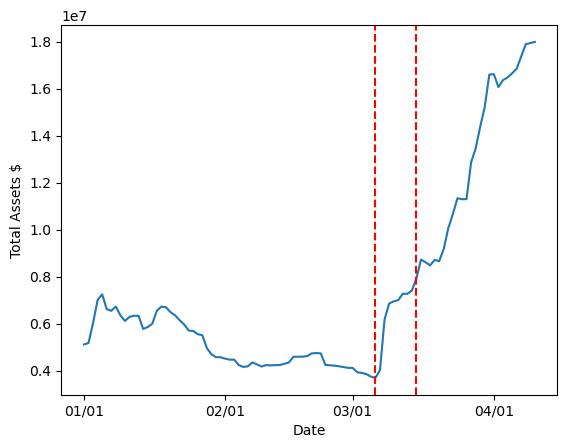
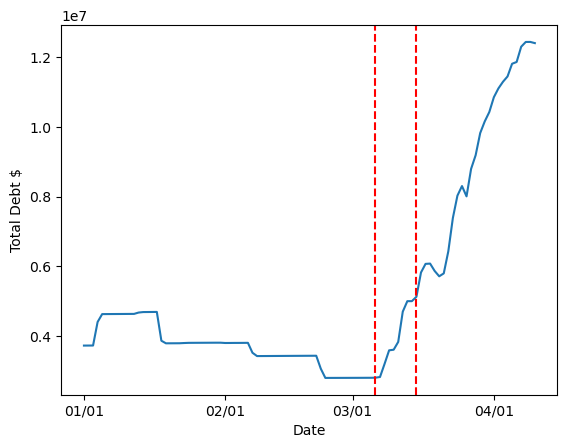
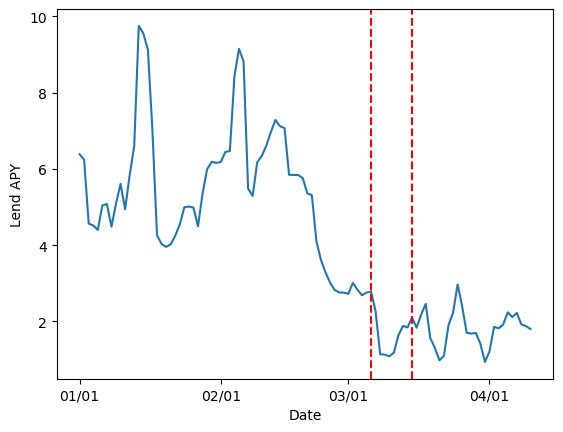
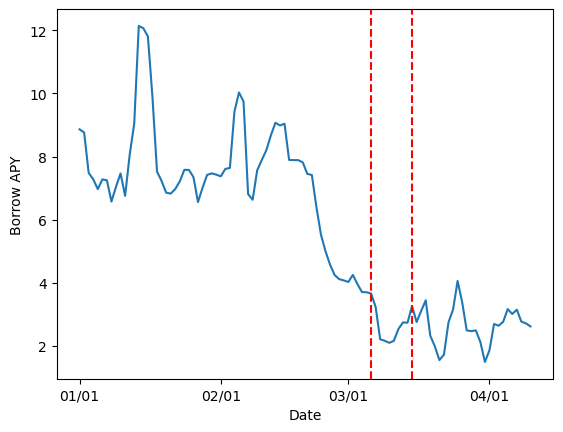
The following plot illustrates total assets, total debt, and utilization over time:
Optimal Utilization Analysis
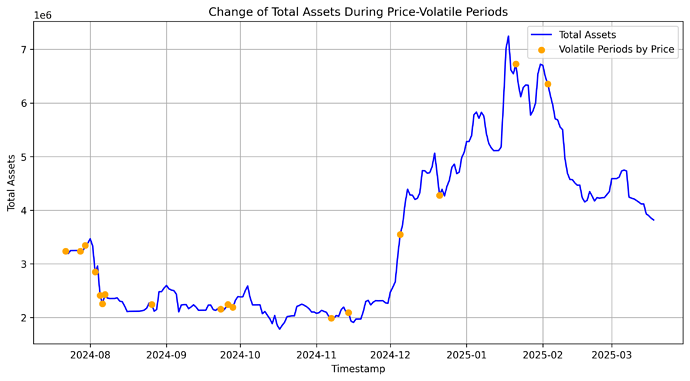
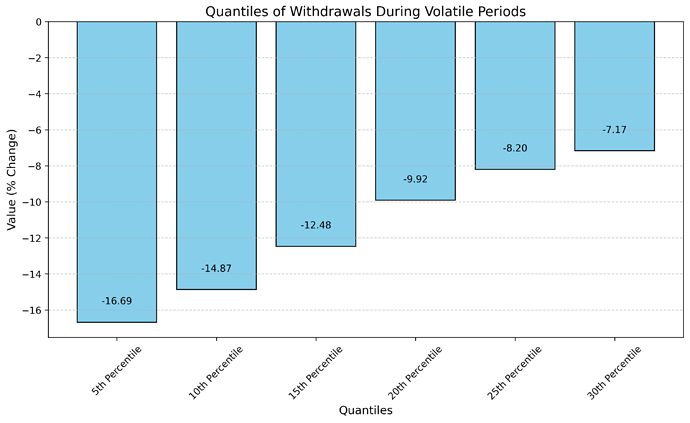
First we determine a target utilization for the market according to historical market data. We analyzed volatile periods, identified through the oracle price feed, and measured asset withdrawal behavior during volatile periods:
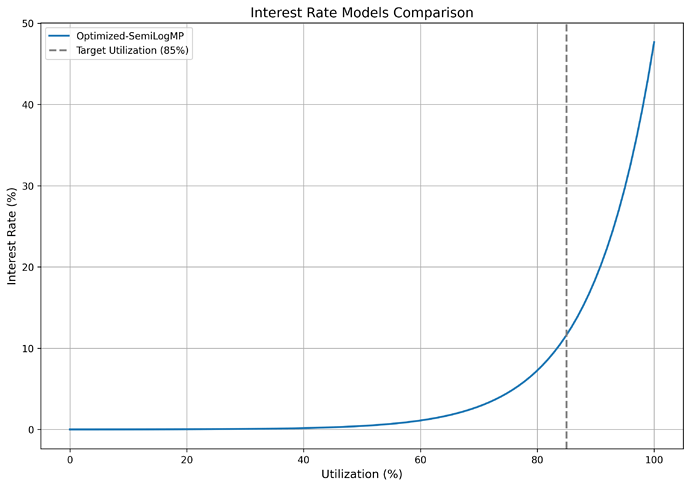
During volatility, the 10th percentile of negative withdrawals of supplied crvUSD was 85%, indicating 90% of withdrawals stayed within this bound. Thus, optimal utilization is conservatively set at 85%, calculated as min(1 - withdrawal_quantile, 0.85).
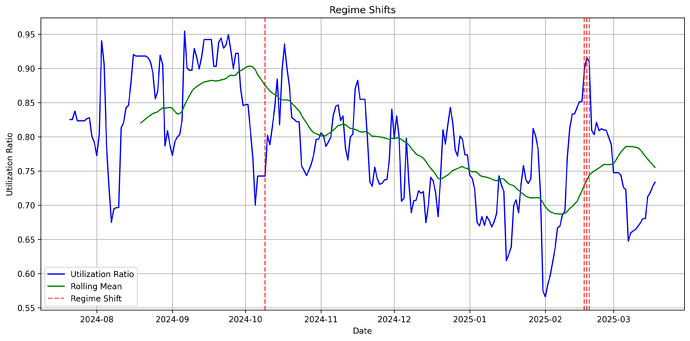
Regime Shift Detection
Significant regime shifts in utilization dynamics (marked by red vertical lines below) indicate changes in market stability, indicating thresholds when the market may require reparameterization:
The last stable regime shift was observed on 2024-10-09. Our analysis spans until 2025-02-17 (131 days), excluding the latest period due to insufficient data for reliable parameter estimation.
Below, we compare empirical utilization against the optimal target within the selected regime:
The selected regime shows, on average, a slight underutilization (76%) relative to the determined optimal level (85%).
Stochastic Parameter Estimation
We applied Ordinary Least Squares (OLS) regression to estimate parameters for our stochastic differential equation:
OLS Regression Results
==============================================================================
Dep. Variable: delta_utilization R-squared: 0.065
Model: OLS Adj. R-squared: 0.057
Method: Least Squares F-statistic: 8.303
Date: Tue, 18 Mar 2025 Prob (F-statistic): 0.00470
No. Observations: 121 AIC: -527.0
Df Residuals: 119 BIC: -521.5
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 0.0197 0.007 2.703 0.008 0.005 0.034
borrow_apr_lag -0.1710 0.059 -2.881 0.005 -0.289 -0.053
==============================================================================
Omnibus: 1.609 Durbin-Watson: 1.818
Prob(Omnibus): 0.447 Jarque-Bera (JB): 1.182
Skew: 0.031 Prob(JB): 0.554
Kurtosis: 3.480 Cond. No. 24.3
==============================================================================
The regression indicates a statistically significant and robust relationship. Assuming we are able to capture the response in utilization by rate for the market, currently referencing an external market through the SecondaryMP, estimates should produce a reasonable evolution of utilization paths.
Optimal Parameter Identification
Using a composite loss function optimized over multiple stochastic simulations, we identified the following optimal parameters for the Semilog IRM:
| IRM Label | rate_min | rate_max |
|---|---|---|
Optimized-SemiLogMP |
0.00004 |
0.47658 |
Parameter Performance Evaluation
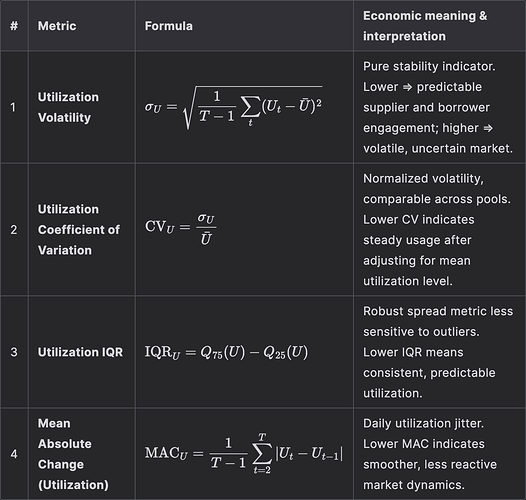
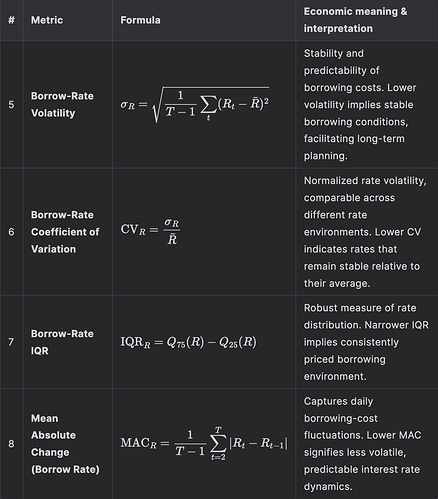
The optimized parameters demonstrate the following performance across key metrics:
Resulting optimized interest rate curve and target utilization:
Conclusion
Switching from SecondaryMP to a semilog IRM for sUSDe offers several clear advantages:
- Eliminates Arbitrary Rate Caps: Ensures borrowing costs can reflect actual market risk.
- Strengthens Market Health: Encourages quicker repayment when conditions worsen, reducing the risk of illiquidity.
- Prioritizes Lender Protection: Reduces opportunities for bad actors to exploit artificially low APRs in times of stress.
By allowing the market to determine interest rates more naturally, LlamaLend can mitigate risk effectively, preserve liquidity, and maintaining a stable lending environment—even under volatile conditions.
Specification
SUSDE_CONT = '0xB536FEa3a01c95Dd09932440eC802A75410139D6'
MONPOL = '0xb8CeDa456f8191d8D0d5b196C7BAab87A309ea50'
ACTIONS = [
# sUSDe Sec MonPol to Semilog
(SUSDE_CONT, "set_monetary_policy", MONPOL),
]